Mathematics in India in the Ancient Times

Consider any number, say 38,50,937. This stands for 3×10,00,000+ 8×1,00,000 + 5×10,000 + 0×1,000 + 9×100 + 3×10 + 7. This is a particular way of expressing a number using the ‘decimal place value system’, where there are 10 digits, 1, 2, …, 9 and 0, and the value of a digit in any number depends on its place. For example, the leftmost digit, 3, in the number above has the value 30,00,000, whereas the digit 3, which is second from right, has the value 30. This scheme is far simpler than other ways of representing numbers used in the ancient past.

The decimal place value system, which is extremely convenient for mathematical operations, gradually developed in India beginning with the Vedic period. For instance, in a verse in the Shukla Yajurveda (prior to 1,500 BCE), numbers are being increased from one to one trillion by taking progressively higher powers of ten: eka (1), dasha (10), shata (102 =100), sahasra (103 =1000), ayuta (104), niyuta (105), prayuta (106), arbuda (107), nyarbuda (108), samudra (109), madhya (1010), anta (1011), and paraardha (1012). Some scholars see in the term lopa (absence, disappearance) of Paanini’s Ashtaadhyaayi, a concept analogous to zero. Philosophical works such as Vyaasabhaashya on Yogasutra refer to the way the same symbol acquires different meanings in the place value system. This along with the notion of zero led to the decimal place value system.

It has been acclaimed universally. The great French mathematician-physicist-astronomer of the 18th century, Simon Laplace, exclaims thus: “It is India that gave us the ingenious method of expressing all numbers by means of ten symbols, each symbol receiving a value of position as well as an absolute value … Its very simplicity and the great ease which it has lent to all computations put our arithmetic in the first rank of useful inventions. …” It is thanks to this very efficient system that Indians excelled in the fields of arithmetic, algebra, trigonometry and astronomy in the past. Shulbasutras were manuals for constructing altars of prescribed sizes and shapes, where Vedic sacrifices would be performed. In Sanskrit, shulba means ‘rope’ (for measurement) and sutras are ‘rules’, so shulbasutras mean ‘rules for measurement with ropes’. Baudhaayana, Aapastamba, Kaatyaayana and Maanava are some of the important ones.

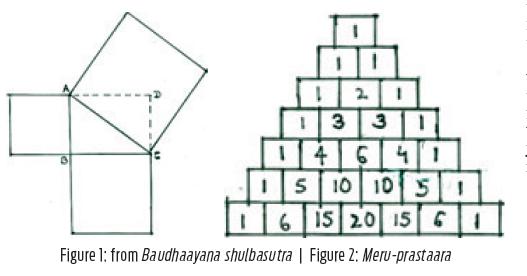
Their mathematical part deals with the construction of squares, rectangles, transformation of geometrical figures, finding the areas of sacrificial altars, etc. Baudhaayana shulbasutra is considered the oldest among them, and is estimated to be composed around 800 BCE A very clear statement of the so-called Pythagoras theorem is to be found in all the aforementioned texts. The Baudhaayana version is: “The [square on the] rope corresponding to the diagonal of a rectangle makes whatever is made by the [squares on the] lateral and vertical sides individually.” In the rectangle ABCD in Figure 1 below, the square on the diagonal AC is the sum of the squares on the sides AB and BC. This is the earliest statement of the theorem anywhere in the world, and before Pythagoras. It is the cornerstone of geometry and is of fundamental importance.

The shulbasutras discuss methods for constructing a square whose area is the sum or difference of the areas of two given squares, or is n times that of a given square, transformation of a rectangle to a square with the same area, (approximately) ‘squaring a circle’, etc., using ropes only. The solutions involve the knowledge of both geometry and algebra. Baudhaayana shulbasutra also gives an approximation for √2 correct to five decimal places: √2 ≈ 1 + (1/3) + (1/3×4) − (1/3×4×34) = (577/408).

In fact, 5772 − (2×4082) = 1, so neglecting 1, we have 2 ≈ (5772/4082) , or √2 ≈ (577/408). It is possible that Baudhaayana was aware of this, or had a geometrical method for obtaining the approximation. Then, there was Pingala’s Chandah-sutra (around 300 BCE) that systematised the rules for the ‘metres’ in Sanskrit poetry, and also discusses the associated mathematics. It uses combinatorial tools and what amounts to a binary representation of numbers for this. A syllable can be laghu (light), or guru (heavy). What is the number of metrical forms with gurus (or laghus) in a prastaara (layout) of metres with n syllables? This is the number of ways in which r objects can be chosen out of n objects and is called the binomial coefficient. Pingala’s sutra on this is all too brief.

Halaayudha, the tenth century commentator, explains it as giving the basic rule for the construction of a table of numbers, which he refers to as the Meru-prastaara that is given in Figure 2. This is a rotated version of the so-called Pascal triangle. It is based on the principle that a number in any row is the sum of the numbers on the two sides of it in the previous row. If we take the last row, 6 = 1+5, 15 = 5+10, 20 = 10+10, and so on. In other words, if we have six objects, there is only one way of choosing none or all the six objects, six ways of choosing one or five objects, 15 ways of choosing two or four objects, and 20 ways of choosing three of them. (This is the second article in the series on India’s contributions to science and technology. Email: sriram.physics@gmail.com)

M S Sriram Theoretical Physicist and President, Prof. K.V. Sarma Research Foundation

Source: The Indian Express

Image Courtesy: VedicFeed